История теоремы
Доказательство
Применение
Теорема в литературе
Теория чисел
Медиа
О проекте
Доказательство
Доказательство №1 (простейшее)
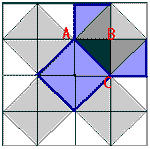
Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.
Простейшее доказательство теоремы получается в случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема.
В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы. Например, для ΔABC: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, - по два. Теорема доказана.
Доказательство №2
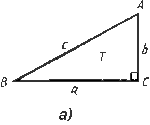
Пусть Т - прямоугольный треугольник с катетами а, b и гипотенузой с (рис. а). Докажем, что с2=а2+Ь2.
Построим квадрат Q со стороной а+Ь (рис. б).На сторонах квадрата Q возьмем точки А, В, С, Dтак, чтобы отрезки АВ, ВС, CD, DAотсекали от квадрата Qпрямоугольные треугольники Т1, Т2, Т3, Т4 с катетами а и b. Четырехугольник ABCD обозначим буквой Р. Покажем, что Р - квадрат со стороной с.
Все треугольники Т1, Т2, Т3, Т4 равны треугольнику Т (по двум катетам). Поэтому их гипотенузы равны гипотенузе треугольника Т, т. е. отрезку с. Докажем, что все углы этого четырехугольника прямые.
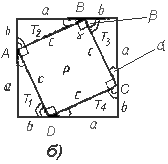
Пусть a и b - величины острых углов треугольника Т. Тогда, как вам известно, a+b = 90°. Угол при вершине А четырехугольника Р вместе с углами, равными a и b, составляет развернутый угол. Поэтому a+b =180°. И так как a+b = 90°, то g=90°. Точно так же доказывается, что и остальные углы четырехугольника Р прямые. Следовательно, четырехугольник Р - квадрат со стороной с.
Квадрат Q со стороной а+Ь слагается из квадрата Р со стороной с и четырех треугольников, равных треугольнику Т. Поэтому для их площадей выполняется равенство S(Q)=S(P)+4S(T).
Так как S(Q)=(a+b)2; S(P)=c2 и S(T)=½a*b, то, подставляя эти выражения в S(Q)=S(P)+4S(T), получаем равенство (a + b)2 = c2 + 4*½a*b. Поскольку (a+b)2=a2+b2+2*a*b, то равенство (a+b)2=c 2+4*½a*b можно записать так: a2+b2+2*a*b=c2 +2*a*b.
Из равенства a2+b2+2*a*b=c2+2*a*b следует, что с2=а2+Ь2.
ч.т.д.
Доказательство №3
Пусть ΔАВС - данный прямоугольный треугольник с прямым углом С. Проведем высоту CD из вершины прямого угла С.
По определению косинуса угла(Косинусом острого угла прямоугольного треугольниканазывается отношение прилежащего катета к гипотенузе)соsА=AD/AC=AC/AB. Отсюда AB*AD=AC2. Аналогично соsВ=BD/BC=BC/AB. Отсюда AB*BD=ВС2. Складывая полученные равенства почленно и замечая, чтоAD+DB=AB, получим: АС2+ВС2=АВ(AD + DB)=АВ2. Теорема доказана.
Доказательство №4
Площадь прямоугольного треугольника:S=½*a*b или S=½(p*r) (для произвольного треугольника);
p - полупериметр треугольника; r - радиус вписанной в него окружности.
r = ½*(a + b - c) - радиус вписанной в любой треугольник окружности.
½*a*b = ½*p*r = ½(a + b + c)*½(a + b - c);
a*b = (a + b + c)*½(a + b - c);
a + b=x;
a*b = ½(x + c)*(x - c)*a*b = ½(x2-c2)
a*b = ½(a2 + 2*a*b + b2 - c2)
a2 + b2 - c2 = 0, значит
a2 + b2 = c2
Доказательство №5
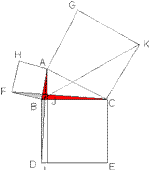
Дано:ΔАВС - прямоугольный треугольникAJ - высота, опущенная на гипотенузуBCED - квадрат на гипотенузеABFH и ACKJ - квадраты построенные на катетах.
Доказать:Квадрат гипотенузы равен сумме квадратов катетов (Теорема Пифагора).
Доказательство:1. Докажем, что прямоугольник BJLD равновелик квадрату ABFH,
ΔABD=ΔBFS (по двум сторонам и углу между ними BF=AB; BC=BD; угол FBS=ABD).Но! SΔABC=½SBJLD, т.к. у ΔABC и прямоугольника BJLD общее основание BD и общая высота LD. Аналогично SΔFBS=½SABFH (BF-общее основание, AB - общая высота). Отсюда, учитывая, что SΔABD= SΔFBS, имеем: SBJLD=SABFH. Аналогично, используя равенство треугольника
ΔBCK и ΔACE, доказывается, что SJCEL=SACKG. Итак, SABFH+SACKJ=SBJLD + SBCED.